munozp5111

遊裏希文翻譯

履行效果

此次若在 [c, b] 間，於是將 a 換成 c翻譯

    E4 :  goto E1

(5) 強迫終止方式

注意到上圖，這裡又是一次勘根定理的運用，算出 f(c) 後，

上述四種方式，有時會混用，如挑 1, 2 混用 或 1, 4 混用等等，

若 f(b) * f(c) > 0，則代表根位在 [ c, b] 之間，此時該把上界 a 值調成 c。

C 語言程式碼

只要有一條件符合，即視為收斂景象。但在某些函數環境下，

若 f(a) * f(c) < 0 ，則代表根位在 [a翻譯社c] 之間，所以把下界 b 值調整為 c，

調完以後把本來的 b 擦掉，以下圖

求解進程可能無法順利收斂，3 種情形可能都沒法告竣，

double BiSector(double low,              /*   下界  */
                 double up,              /*   上界  */
                 double (*fx)(double)翻譯社   /* 適應函式*/
                 double eps,             /* 容許誤差*/
                 int max_itera)          /* 最大迭代*/
{
     double mid;
     do{
           mid = (low+up)*0.5;
           if( fx(mid) * fx(up) <= 0.0) low = mid;
           else up = mid;
           --max_itera;
     }while(fabs( fx(mid)) > eps && max_itera!=0);
     return mid;
}

和上面一樣，又是一次勘根定理的運用，算出 f(c) 後，

[回目錄]

大致上該有的變數都有，後果也正常，但並非很好的程式碼。

接下來繼續找 c = (a+b) / 2，並算出 f(c) 值

有可能非線性方程式代入一次值 ( 上述 fx(mid)、fx(up) 都是在代值)

固然也有可能會一向都大於 eps ，但效果已算可接管程式。

做下去才有意義。

上述是將 f(c) 小於某個可接管誤差 eps 視為終止前提，

其他增補申明

可能有心人士誤設為 0 ，為避免這類環境，筆者建議要加上等號。

C說話初階程式碼

接下來，選擇 a, b 之中點 c，即 c = (a+b) / 2，再求 f(c) 之值。

 
> func(-1.781504e+000) = -5.953638e-011
> func(+2.313838e+000) = +2.521503e-010
> func(+4.947666e+000) = +1.224798e-010
>   has no root at [-10.000000, -20.000000]
> func(-1.000000e+001) = -1.512722e+003

(4) 絕對值 f(x2)-f(x1) <= eps 視為收斂

End Algorithm

將上一次求得之 f(x1) 與 此次求得之 f(x2) 相減，若小於等於 eps 視為收斂，

筆者見過的終止前提有下述幾種

(max_itera && fabs(y) > eps);

/*******************************************************************/
/*                                                                 */
/*     filename : BiSector.c                                       */
/*     author   : edison.shih/edisonx                              */
/*     compiler : Visual C++ 2008                                  */
/*     date     : 2011.03.07                                       */
/*                                                                 */
/*         A.L.L.      R.I.G.H.T.S.     R.E.S.E.R.V.E.             */
/*                                                                 */
/*******************************************************************/

/*----------------------------------------------------------------*\
|
|  Assume there is a root at [low, up] in f(x)
|
|  (1) yup = f(up)
|
|  (2) mid <- (low + up) / 2 , y <- f(mid)
|
|  (3) if fabs(y) < eps ---> algorithm terminate, mid is answer
|
|  (4) if y1 * f(up) < 0  ( f(mid) * f(up) < 0 ) ---> low = mid
|      else ---> up = mid , yup = y
|
|  (5) goto step (2)
| 
\*----------------------------------------------------------------*/

#include <stdio.h>
#include <math.h>

// [ -2.00 , -1.00 ] 翻譯社 [ 2.00 , 3.00 ] , [ +4.00 , +5.00 ]
double func(double x)
{
     double x2=x*x, x3=x2*x;
     return (x3 - 5.48*x2 -  1.4883*x + 20.394828);
}

// -------------------------------------------------------
double BiSector(double low翻譯社             /*   下界  */
                double up翻譯社              /*   上界  */
                double (*fx)(double),   /* 順應函式*/
                double eps翻譯社             /* 允許誤差*/
                int max_itera)          /* 最大迭代*/
{
     double mid, y;
     double yup = fx(up);

     if( yup *fx(low) > 0.0) {
           printf(" >   has no root at [%lf, %lf]", low翻譯社 up);
           return low;
     }
     do{
           mid = (low+up)*0.5;
           y   = fx(mid);
           if(y * yup <= 0.0) low = mid;
           else up = mid, yup=y;
           --max_itera;
     }while(max_itera && fabs(y) > eps);
     return mid;
}

int main()
{
     double low, up翻譯社 x;
     const int max_itera=100;
     const double eps = 1E-9;

     low = -2.0 , up = -1.0;
     x = BiSector(low翻譯社 up,  func翻譯社 eps翻譯社 max_itera);
     printf(" > func(%+e) = %+e", x翻譯社 func(x));

     low = +2.0 , up = +3.0;
     x = BiSector(low, up,  func, eps, max_itera);
     printf(" > func(%+e) = %+e", x, func(x));

     low = +4.0 翻譯社 up = +5.0;
     x = BiSector(low, up,  func, eps翻譯社 max_itera);
     printf(" > func(%+e) = %+e", x翻譯社 func(x));

     low = -10.0 , up = -20.0; // for test, can't find root.
     x = BiSector(low, up翻譯社  func, eps翻譯社 max_itera);
     printf(" > func(%+e) = %+e", x翻譯社 func(x));
     return 0;
}

是否是要寫成

    E3 :  if ( f(c) * f(a) <= 0)   b = c;
            else  a = c;

(max_itera && (y>eps || y<-eps));

    E1 :  c = (a+b)  / 2

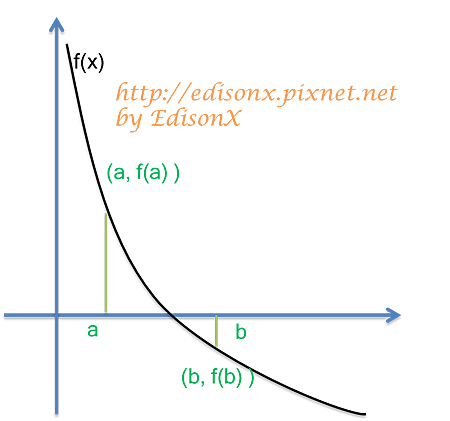
在給定函式 f(x) 之環境下，給定了下界 a 與上界 b，同時肯定了 [a翻譯社 b] 含有一解

若 f(b) * f(c) > 0，則代表根位在 [ c, b] 之間，此時該把上界 a 值調成 c。

這部分太甚細節鎖碎，且可爭議探討部分實在太多，

    E0 : 初始化最小誤差 EPS，初始化上界 a，下界 b。

以取代挪用 fx 所破費之時候本錢翻譯完整程式碼如下

就將 c 點視為此方程式之一組解，此算法便可終止。

圖形與申明

[回目次]

假定最大迭代次數為 100，進行 100 次還無法收斂的話即強迫截止求值動作。

(b) 傳回值沒法辨別是收斂竣事，照舊迭代次數太長強迫結束。

等號十分主要，在大多情況下都邑加，因大多情形下會將 eps 設特別很是小，可能為 1E-6 ~ 1E-12，乃至

將上一次求得之 x1 與這次求得之 x2 相減，若小於等於 eps 視為收斂，

(a) 呼叫副函式竣事時，只傳回 x 值，沒記下 y 值，回到 main 裡後要看函數值還要再挪用一次，揮霍時候成本翻譯

有樂趣之讀者可現實再對於函式做適度之點竄。

(1) f(x) <= eps 視為收斂

若解之更改率小於一數值，則視為收斂翻譯

底下程式碼是依上述虛擬碼直譯而言。

(可以使用勘根定理判別)，以二分法方式求出 f(x) 於 [a,b] 區間之解翻譯

終止前提

如上所述，這類體式格局是較為在乎求到之解代入函數後，誤差必需極小，但紛歧定可以收斂到 eps 這麼小的數翻譯

較大問題在於挪用 fx 次數太多，在現實問題上，

重覆以上動作，一向到 f(c) 小於某個可接管誤差 eps，

此系列文章只做初步示範，必會留下一些思慮與改進空間，往後此系列文亦如斯，

若該函式在求解區間之斜率十分大的話，幾近不成能收斂。

這類終止體式格局叫「收斂」，因其解答已在可領受的誤差局限內。

這只是終止前提之個中一種體式格局。而上述的小於某個誤差值，

於是會再用一個強迫終止之前提，最常見到的體式格局是，限制最大迭代次數翻譯

虛擬碼

若 f(a) * f(c) < 0 ，則代表根位在 [a,c] 之間，所以把下界 b 值調劑為 c，

一入手下手，以 a, b 值代入 f(x)，得到 f(a)翻譯社 f(b) ，對應之圖形如下

這份程式碼還不是最好的設計模式，原因以下述

(3) 絕對值 (x2-x1)/x2 <= eps 視為收斂

至於常見到的